Physics meets economics: The gravity equation in international trade
In this post I introduce the concept of gravity in economics, which is similar to physics. I use some data visualisation of trade from Australia and the UK to demonstrate gravity as a fact and how it fits with modern theories of international trade.
International trade has always been a topic of heated ideological debate among non-economist, politicians and even for economists that are not trade specialists. Take the example of Brexit or your local country that brings legislations to promote Free Trade Agreements (FTA). You will always see strong position against or in favour of these trade policies, however most people do not know that countries have an implicit inclination to have more trade between them when they are closer to each other . This concept is called the “gravity equation”. The equation was given its name by a Dutch economist and Nobel laureate, Jan Tinbergen. Tinbergen was trained in physics, so he thought about the trade between countries as similar to the force of gravity between objects: Newton’s universal law of gravitation states that objects with larger mass, or that are closer to each other, have a greater gravitational pull between them. Tinbergen’s gravity equation for trade states that countries with larger GDPs, or that are closer to each other, have more trade between them.
The equation has three components. Trade is the amount of trade (measured by imports, exports, or their average), GDP1 and GDP2 are their gross domestic products, and dist is the distance between them. The term B is a constant that indicates the relationship between Trade and the “gravity term”. B summarises the effects of all factors (other than size and distance) that influence the amount of trade between two countries; such as tariffs, FTA, common language, etc.
Gravity of Australian total trade
The data are for Australia merchandise exports to 188 countries in 2017 (the latest full year for which comparable data are available). Figure 1 plots Australia exports against importer GDP, both in logs of current dollars. The positive relationship between the two is apparent, and confirmed by the simple regression line. The estimated slope coefficient is 0.98 with a standard error of 0.06: significantly different from zero but not from one. Most theoretical foundations of the gravity equation assume that this coefficient equals one.
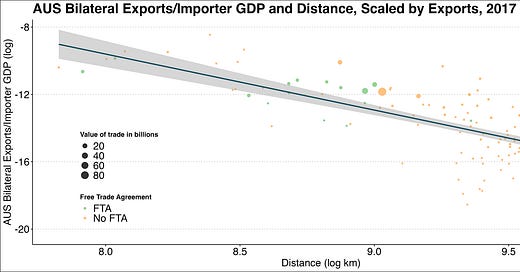
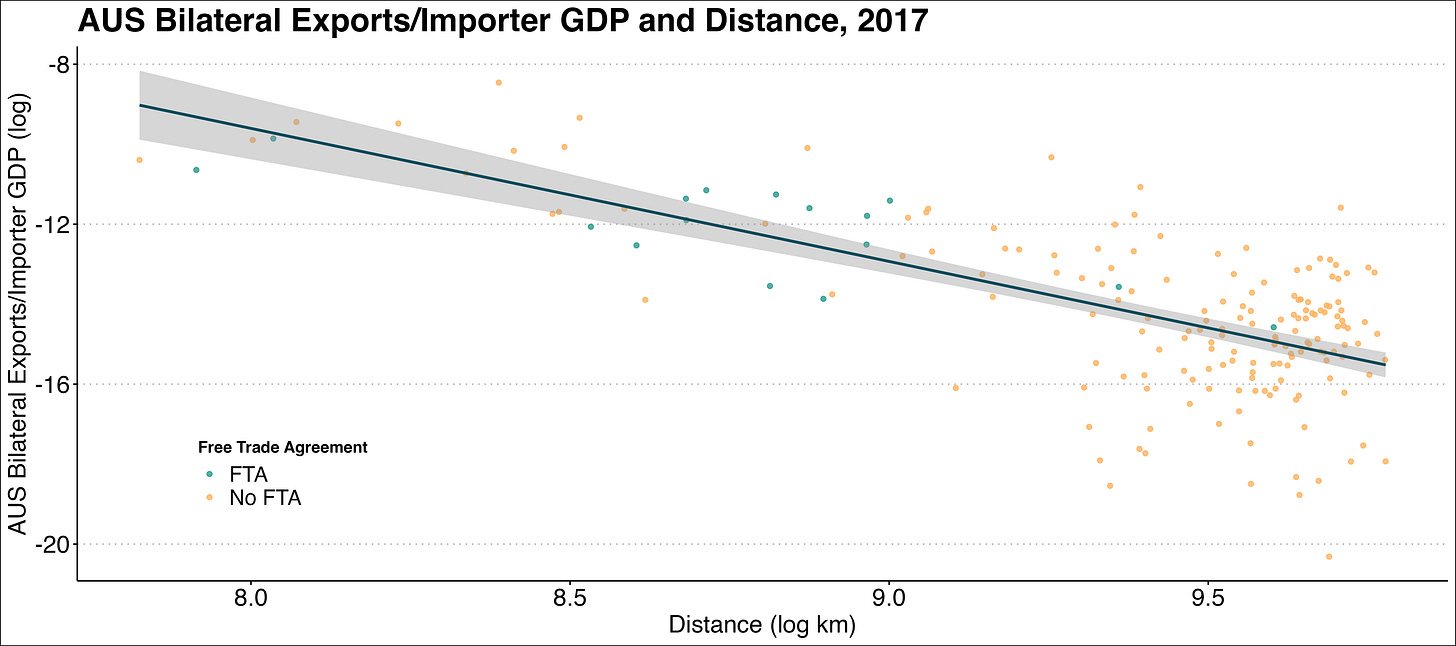
Figure 2 plots this ratio against bilateral distance, both once again in logs. This time the simple regression line is downward-sloping. Its estimated slope coefficient is -3.38 with a standard error of 0.284: significantly from zero. For each export market, the dots indicate its trading relationship with Australia as of the end of 2015: a blue dot if it is a regional trade area, a yellow if not.
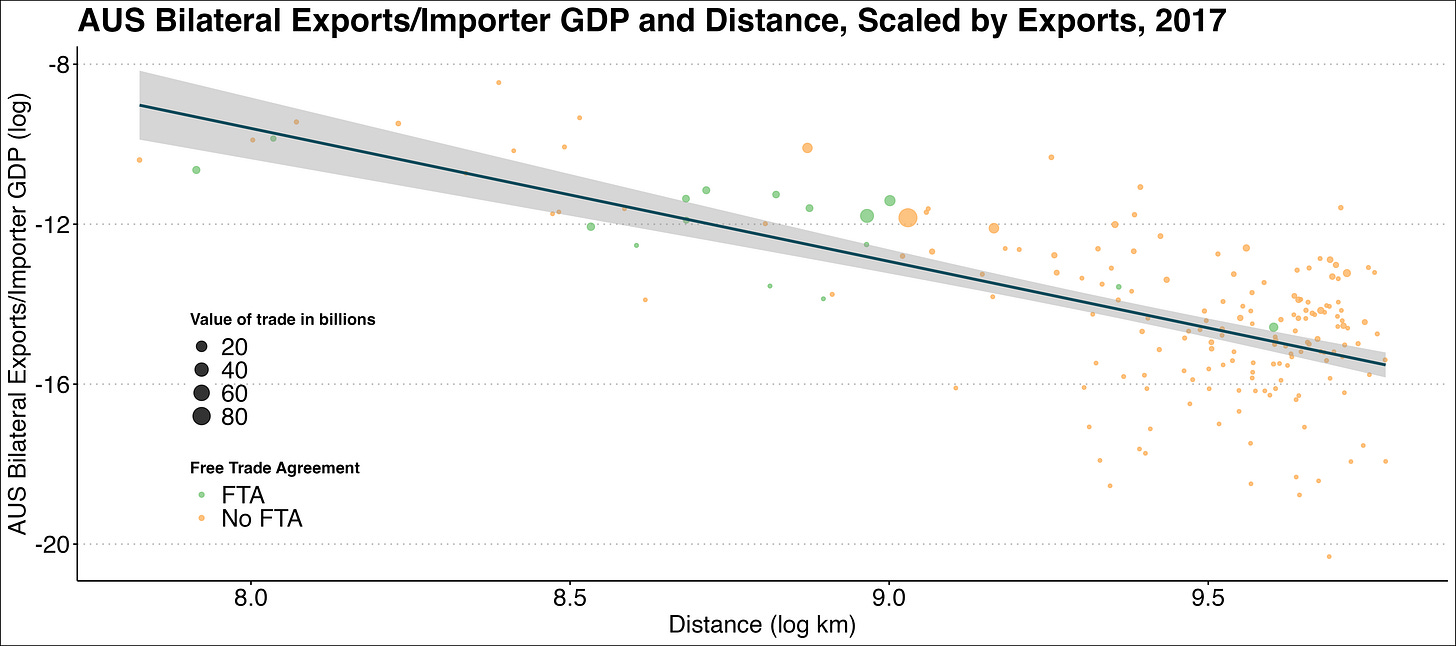
Figure 3 illustrates the same data as Figure 2 but this time with the size of each observation proportional to the share of Australia exports to that country. Figures 2 and 3 indicate that Australia trade falls with distance, when we control for the size of the importing country. Figure 3 also shows that the tendency to cluster around the best-fit line is even more pronounced for larger trading partners. Most of the largest export market lie on or close to the best-fit line and many extreme outliers are very small when we scale by the share of exports. This is not unique to Australia and it seems that Australia do not have many FTAs in force so I will replicate figure 3 to the UK before Brexit instead to reinforce my point.
Gravity of UK total trade
As you can see in figure 4 the UK has more FTAs and some are with countries with small levels of trade. This is because FTA accounts for EU members and non-EU members. Most EU members are the dark blue dots on the top left side of figure 4. This pattern reinforces the point of the gravity equation that trade falls with distance. However, it is not only geographical distance that matters in gravity equations. Distance in other senses affects trade, with variables such as common language, legal system, colonial origins and so on. For the UK, it could have been useful for trade policy before Brexit because it enjoyed free and frictionless trade with EU countries instead of negotiating new trade agreements with the far-away circles in the graph.
Gravity has an important role in international trade. There is an overwhelming evidence that trade tends to fall with distance, as even a superficial examination of Australia and the UK export patterns confirm. There is a vast theoretical work related to gravity models consistent with Ricardian comparative advantage and monopolistic competition with heterogeneous firms. Finally, I want to say that this post was inspired by professor J. Peter Neary after watching his presidential address at the Royal Economic Society. Sadly, he passed away in June and this is a tribute to him and his work. Professor Neary was an eminent trade economist with many influential contributions among them his classic paper on Deindustrialization and the Dutch Disease published in the Economic Journal.